1. Overview of continuity of functions of two variables
-
Section 1.We discuss two standard exercises on continuity and discontinuity of real functions in real variables.
-
Section 2.We list the definitions of the functions discussed in all the exercises that can be found in the text document that the reader can download.
-
Section 3.The reader can download the text document in the download section.
-
Section 4.The reader can find information about web based material in the information section about links and search material .
2. Continuity of functions in two real variables: exercise notes
We discussed in the past with students a few standard examples of exercises about continuity and discontinuity of real functions of two variables and have collected the exercises in a text document. This text can be downloaded. Some examples of exercises are standard examples and can be found in many texts.
We think that the text can be useful for everyone studying the theory of functions in two variables for the first time. The text is certainly not aimed only at students with a mathematics major. We think that the general public studying a calculus text can make use of it.
2.1 Two standard exercises
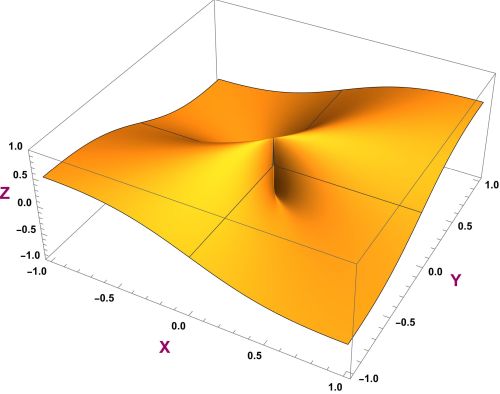
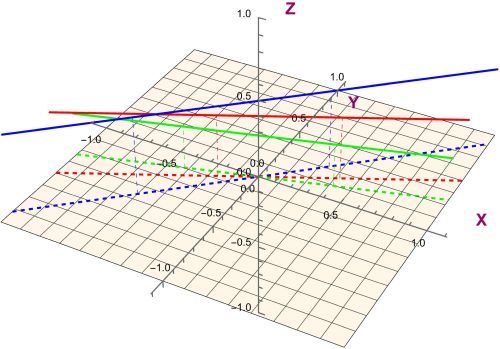
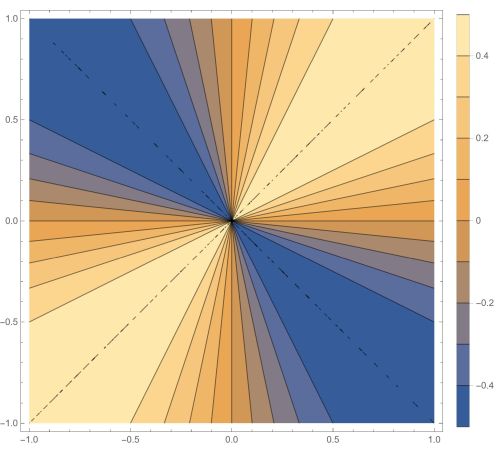
Is the function continuous in ?
Solution.
Let us calculate the function restricted to a line . We have in that case:
We calculate the limits. This gives us an infinite amount of different limit values for the function restricted to the different lines. If the function is continuous, then all these values should give us the function value in , that is . So this function is not continuous.
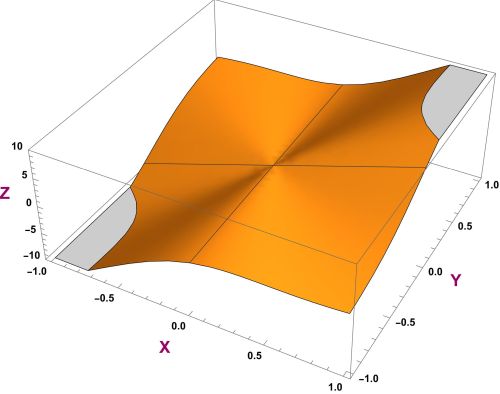
Is the function continuous in ?
By looking at our function, we have in our case the following statements. Try to find a such that if , we have that
We are looking for a function that is larger then or equal to the left hand side of this last inequality. This function has to have the property that it can be made smaller then by carefully manipulating the value . This is sufficient for our continuity proof.
It is sufficient to prove that by manipulating the magnitude of in the inequality . We can choose for example with . We have found a and the function is indeed continuous.
2.2 List of exercises
|
Exercise 1.
|
|
Exercise 2.
|
|
Exercise 3.
|
|
Exercise 4.
|
|
Exercise 5.
|
|
Exercise 6.
|
|
Exercise 7.
|
|
Exercise 8.
|
|
Exercise 9.
|
|
Exercise 10.
|
|
Exercise 11.
|
|
Exercise 12.
|
|
Exercise 13.
|
|
Exercise 14.
|
|
Exercise 15.
|
|
Exercise 16.
|
|
Exercise 17.
|
|
Exercise 18.
|
|
Exercise 19.
|
|
Exercise 20.
|
|
Exercise 21.
|
|
Exercise 22.
|
|
Exercise 23.
|
|
Exercise 24.
|
|
Exercise 25.
|
|
Exercise 26.
|
|
Exercise 27.
|
|
Exercise 28.
|
|
Exercise 29.
|
|
Exercise 30.
|
|
Exercise 31.
|
|
Exercise 32.
|
|
Exercise 33.
|
|
Exercise 34.
|
|
Exercise 35.
|
|
Exercise 36.
|
|
Exercise 37.
|
|
Exercise 38.
|
|
Exercise 39.
|
|
Exercise 40.
|
|
Exercise 41.
|
|
Exercise 42.
|
|
Exercise 43.
|
|
Exercise 44.
|
|
Exercise 45.
|
|
Exercise 46.
|
|
Exercise 47.
|
|
Exercise 48.
|
|
Exercise 49.
|
|
Exercise 50.
|
|
Exercise 51.
|
|
Exercise 52.
|
|
Exercise 53.
|
|
Exercise 54.
|
|
Exercise 55.
|
|
Exercise 56.
|
|
Exercise 57.
|
|
Exercise 58.
|
|
Exercise 59.
|
|
Exercise 60.
|
|
Exercise 61.
|
|
Exercise 62.
|
|
Exercise 63.
|
|
Exercise 64.
|
|
Exercise 65.
|
|
Exercise 66.
|
|
Exercise 67.
|
|
Exercise 68.
|
|
Exercise 69.
|
|
Exercise 70.
|
|
Exercise 71.
|
|
Exercise 72.
|
|
Exercise 73.
|
|
Exercise 74.
|
|
Exercise 75.
|
|
Exercise 76.
|
|
Exercise 77.
|
|
Exercise 78.
|
|
Exercise 79.
|
3. Download the exercises text
The text document “Exercise notes on the continuity of functions of two variables” with all the exercises and solutions can be viewed online and optionally downloaded. This is a file in pdf format. The text document is not small though: the size is about 47 megabytes due to many illustrations. The illustrations have a resolution of the industry standard 270 DPI. This enables the reader to reasonably enlarge it to see more detail. The text will also be ready to be printed on high resolution devices if necessary.4. Links
A good place to start is always wikipedia.
Because the subject of continuity in two variables is frequently discussed and continuously changed on the net, we can perhaps advise to use your favourite search machine with a search string of something like continuity functions two variables.
https://www.google.com/search?q=continuity+functions+two+variables
- https://math.stackexchange.com/questions/1486308/finding-weird-examples-of-continuous-functions-or-maybe-theyre-tricks
- math.stackexchange.com: questions on continuity with two variables.
- math.stackexchange.com: continuity of a two variable function.
- math.stackexchange.com: questions on continuity in functions with 2 variables.
- math.stackexchange.com: questions on condition for continuity two variable.
- math.stackexchange.com: questions on continuity of functions of two variables.
- math.stackexchange.com: questions on the continuity of a function of two variables, how can we determine it exists.
- mathoverflow.net: questions on the continuity of lipschitz constant over multivariable function.
- physicsforums.com: two variable limit.
- physicsforums.com: continuity of piecewise function of two variables.
We use our favourite search machine with for example the search string
multivariable calculus continuity functions two variables.
We can change the search string at leisure.
Here are some websites with explanations about the continuity of functions in two variables.
- Opentextbc.ca: calculusv3openstax, chapter limits and continuity.
- math.libretexts.org: Limits and Continuity of Multivariable Functions.
- sfu.ca: math coursenotes, Limits, Continuity, Partial Differentiation.
- tutorial.math.lamar.edu, calculus, limits.
- shortinformer.com: how to check the continuity of two variables.
